Calcoli Stellari: Questione di Forza – Starkiller e lo Star Destroyer

Dopo aver mostrato, nel precedente articolo di Calcoli Stellari, che determinati risultati della nostra Matematica si applicano anche all’universo starwarsiano, in questo secondo appuntamento ci dedicheremo allo svolgere dei calcoli partendo dal presupposto che determinate leggi fisiche si applichino anch’esse allo stesso modo tra realtà e finzione. I calcoli in questione riguardano una particolare sequenza presente nel videogioco Legends Star Wars: Il potere della Forza (2008) e ambientata sul pianeta Raxus Prime dove Galen Marek, l’apprendista segreto di Darth Vader conosciuto anche come ‘Starkiller‘, ha dato prova della sua potenza e delle sue abilità con una vera e propria prova di forza.

La vicenda di Starkiller

Per venire incontro a chi non conosce il gioco (il che è legittimo, non essendo più canonico), cercheremo di dare un contesto a questa sequenza in maniera sintetica ma esaustiva.

Ci troviamo poco tempo prima di Episodio IV, nel 2 BBY. Galen Marek, dopo aver dato la caccia ad alcuni Jedi superstiti ed essere stato inizialmente tradito dal suo Maestro, rimane al suo servizio per nuove missioni. Viene infatti incaricato da Darth Vader di fondare l’Alleanza Ribelle per distrarre le spie dell’Imperatore. Per dare maggiore credibilità a questa nuova minaccia, gli ordina inoltre di distruggere il cantiere navale presente sul pianeta Raxus Prime, nel quale venivano costruiti gli Star Destroyer della Flotta Imperiale. Di fatto, Galen compie la sua missione, ma un singolo incrociatore riesce a fuggire dirigendosi verso la superficie del pianeta. L’adepto del Lato Oscuro (che pian piano mostrerà sempre più segni di vicinanza al Lato Chiaro), grazie al “semplice” uso della Forza, riesce a forzare lo schianto della nave e a sbarazzarsene definitivamente.

A questo punto può sorgere spontanea una domanda: con quanta forza (e non Forza) Starkiller provoca lo schianto dello Star Destroyer?

Per rispondere, modellizzeremo la situazione semplificandola il più possibile (di fatto ottenendo una stima per difetto del risultato). Prima, però, risulta doveroso recuperare alcuni concetti fondamentali che ci serviranno per impostare, e infine risolvere, il problema.

Il moto rettilineo uniformemente accelerato e la caduta di un grave

Quando si parla di moto, in Fisica, si fa riferimento a un corpo che si sta muovendo. Un moto può essere classificato in diversi tipi, sulla base dei diversi elementi che lo configurano: direzione, traiettoria, spostamento, velocità, accelerazione, tempo… Prendiamo allora la dicitura “moto rettilineo uniformemente accelerato”, che nel seguito abbrevieremo con la sigla M.R.U.A., e analizziamola per carpire le informazioni sul moto in questione:

• moto → movimento;
• rettilineo → lungo una linea retta (la direzione del moto);
• uniformemente accelerato → è presente un’accelerazione (cioè una variazione della velocità) con valore costante.

Possiamo quindi visualizzare un M.R.U.A. come un movimento diretto lungo una sola direzione e la cui velocità aumenta in maniera costante nel tempo: per dirla in parole povere, e per mettere insieme le informazioni appena estrapolate, più tempo passa e maggiore sarà la velocità del corpo che si sta muovendo.

Un caso particolare di M.R.U.A. è quello dato dalla caduta di un grave, ovvero di un oggetto che viene lasciato cadere sotto l’azione dell’accelerazione di gravità (eventualmente con una velocità iniziale data da una “spinta” verso il basso, almeno in questo caso), la cui legge oraria della posizione (ovvero l’equazione che individua la posizione dell’oggetto in funzione del tempo) è la seguente.

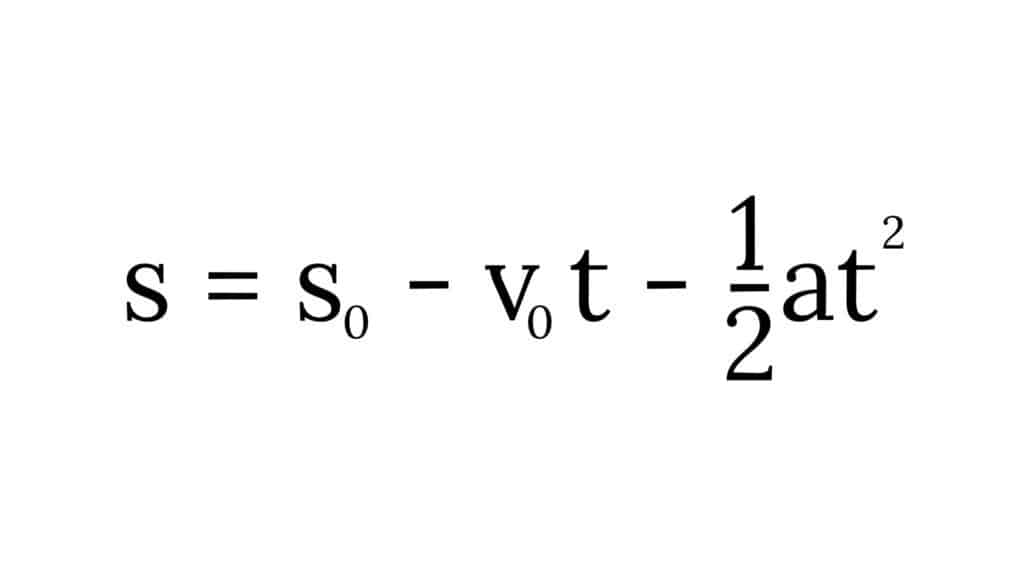
Specifichiamo inoltre che, nell’equazione data:

• t è il tempo;
• s è la posizione all’istante t;
• s₀ è la posizione iniziale;
• v₀ è la velocità iniziale;
• a è l’accelerazione.

Le forze e la Seconda Legge di Newton

Per “forza”, in Fisica, si intende ciò che, all’atto pratico, provoca i moti degli oggetti descrivendone l’interazione con l’ambiente circostante. Un esempio di forza con cui ci si interfaccia quotidianamente è la forza peso: essa consiste nella forza con cui il pianeta Terra ci tiene a sé impedendoci di fluttuare liberamente nello spazio (naturalmente tale concetto si estende anche alla Luna, a Venere e a tutti i corpi celesti di grandi dimensioni); di fatto si tratta di un caso specifico di forza di attrazione gravitazionale.

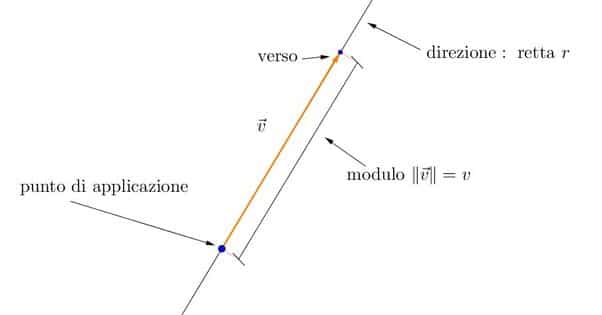
Tornando al caso generale, una forza necessita di quattro caratteristiche in quanto rappresentata da un vettore:

• una direzione (ovvero la retta lungo la quale agisce);
• un verso (vale a dire il modo in cui può essere orientata sulla sua direzione);
• un’intensità (quanto è lungo il vettore che la rappresenta);
• un punto di applicazione (cioè il punto esatto della direzione sul quale agisce).

Ecco un’immagine riassuntiva che illustra graficamente una forza e le sue caratteristiche.

Esiste un legame tra forza e accelerazione? Assolutamente sì, ed è descritto dall’elegantissima relazione che sintetizza la celeberrima Seconda Legge di Newton: “Un corpo di massa m, sotto l’azione di una forza F (eventualmente risultante di più forze agenti sullo stesso corpo), subisce un’accelerazione a nella stessa direzione e nello stesso verso della forza F con intensità direttamente proporzionale a quella della forza F stessa”.

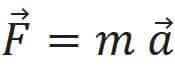
Tale risultato vale a prescindere dalla natura della forza agente sul corpo.

A questo punto abbiamo rivisto tutte le nozioni fondamentali che ci servono, ma prima di impostare il problema, per completezza, andiamo a vedere quali sono le unità di misura delle grandezze fisiche in gioco:

• l’accelerazione è definita come la variazione della velocità nel tempo, e la velocità è a sua volta definita come la variazione della posizione nel tempo, da cui segue che v=[m/s] e a=[m/s²];
• la massa è una proprietà intrinseca di ogni corpo che indica la quantità di materia che lo va a costituire, e si ha m=[Kg];
• la forza, essendo il prodotto di massa e accelerazione, ha come unità di misura il newton, e si ha F=[N]=[Kg･m/s²].

I dati del problema

L’ultimo step necessario per la risoluzione del quesito consiste nel dare delle stime sui valori in gioco, tenendo conto del fatto che non li conosciamo esplicitamente:

• l’altezza a cui si trova lo Star Destroyer inizialmente;
• il tempo che passa da quando Starkiller inizia a usare la Forza sull’incrociatore a quando quest’ultimo si schianta al suolo;
• la massa dello Star Destroyer.

Per quanto riguarda l’altezza iniziale dell’incrociatore imperiale, supponendo si tratti di un classe Imperial I, possiamo valutarla intorno ai 900 m: questo modello di nave, infatti, è alto ben 455 metri, e dal fermo immagine riportato poco sopra, nonostante la prospettiva sia poco pratica per il nostro scopo, possiamo stimare che se ne possano impilare altri due al di sotto del suo ventre (2･455=910 m).

Il tempo che trascorre da quando Starkiller inizia a provocare lo schianto della nave (coincidente con l’inizio della cinematica) a quando quest’ultima tocca il suolo (ovvero in concomitanza con la prima esplosione che si verifica sullo scafo) è di circa 10 s. Potete facilmente verificarlo controllando il timecode dei diversi video reperibili su YouTube che mostrano questa sequenza.

La massa dello Star Destroyer, purtroppo, non è nota né facilmente deducibile dalla cinematica, ed è per questo motivo che chiameremo in nostro soccorso un valido candidato di cui conosciamo effettivamente questo dettaglio e che ci permetterà di stabilire, con una buona approssimazione, quello che stiamo cercando.

Esempio reale

Quello che vedete in foto era l’Antonov An-225 Mriya, un esemplare unico al mondo di aereo da trasporto strategico andato distrutto nei primi giorni del conflitto russo-ucraino. È proprio grazie a esso che daremo una stima della massa dell’incrociatore imperiale: dalla scheda tecnica di questo incredibile velivolo sappiamo che a vuoto aveva una massa di ben 285’000 Kg e una capacità di carico di 250’000 Kg. Sapendo che un Imperial I ha una capacità di carico di 36’000 tonnellate, cioè di 36’000’000 Kg, possiamo impostare una semplice proporzione da cui ricavare la massa dello Star Destroyer:

285’000 : 250’000 = m : 36’000’000.

Da questa uguaglianza otteniamo m= 285’000･36’000’000/250’000=41’040’000 Kg. L’incrociatore ha dunque una massa a vuoto di oltre 40’000 tonnellate, almeno secondo la nostra stima. Per risolvere il problema useremo questo dato, ma tenete conto che il valore reale sarebbe sicuramente maggiore considerando anche la massa dell’equipaggio e degli eventuali veicoli e velivoli presenti nella stiva.

Adesso siamo ufficialmente pronti a impostare e risolvere il problema.

L’impostazione del problema

Per prima cosa rappresentiamo la scena con il relativo schema delle forze, che contiene anche alcuni dei dati a disposizione (non è in scala in quanto non necessario), e, per semplicità, approssimiamo l’incrociatore a un punto materiale (in sostanza le sue dimensioni non contano e la sua massa si pensa concentrata in un unico punto) e trascuriamo l’attrito dell’aria.

Osservate che, nello schema sopra raffigurato, non è presente la forza peso P esercitata da Raxus Prime sullo Star Destroyer. Non temete, non si tratta di un errore: se supponiamo che l’astronave sia ferma inizialmente, stiamo automaticamente dicendo che su di essa non sta agendo alcuna accelerazione; sotto tale ipotesi, sapendo che a=F/m, necessariamente F è nulla, quindi la forza peso P è bilanciata da un’altra forza -P che ha stessa direzione e stessa intensità di P, ma verso opposto. Tale forza, in questo caso specifico, è quella generata dai propulsori della nave che la tengono stabile all’altezza stimata in precedenza.

Tornando all’impostazione del problema, avendo già ricavato tutti gli altri dati necessari, per poter trovare la forza F con cui Starkiller provoca lo schianto dello Star Destroyer ci basta calcolare l’accelerazione del suo moto: possiamo tranquillamente estrapolarla dalla legge oraria del M.R.U.A. mostrata in precedenza esplicitando rispetto ad a.

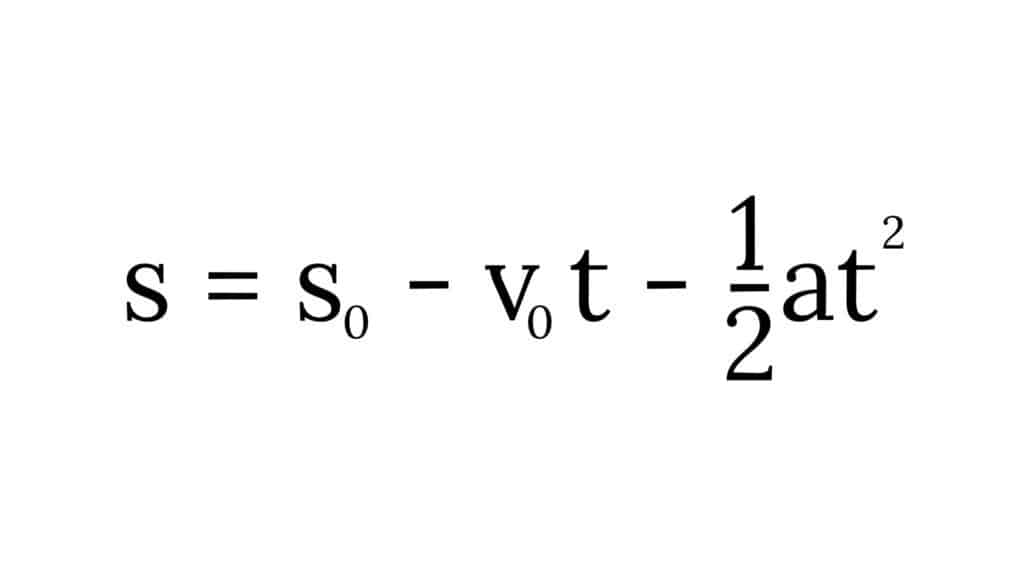
Con una serie di passaggi algebrici elementari, abbiamo la seguente formula.

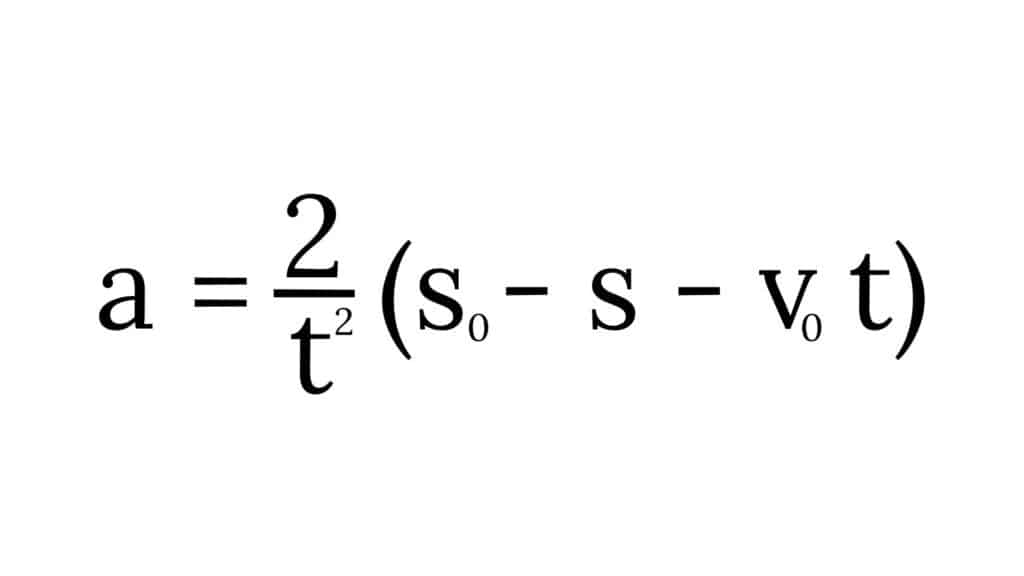
Sostituendo in questa espressione i valori noti, nello specifico:

• t=10 s;
• s₀=900 m;
• s=0 m (vogliamo che la posizione finale dello Star Destroyer sia al livello del terreno);
• v₀=0 (supponendo che lo Star Destroyer fosse fermo prima dell’intervento di Starkiller);

otteniamo il seguente valore di a:

a=2･900/100 m/s²=18 m/s².

Non ci resta altro da fare che svolgere il prodotto m･a per trovare l’intensità di F.

Starkiller e lo Star Destroyer: la soluzione

Svolgiamo dunque questa moltiplicazione e ricaviamo il valore effettivo della forza esercitata da Starkiller: F=(41’040’000 Kg)･(18 m/s²)=738’720’000 N.

Un numero a dir poco mastodontico, parliamo di quasi un miliardo di newton di forza; ma, concretamente, c’è qualcosa con cui rapportare questo risultato? Ebbene sì: vi basti infatti pensare che la forza con cui Starkiller provoca lo schianto dello Star Destroyer è pari a circa 179 volte la forza con cui la Terra attrae a sé l’I.S.S. (Stazione Spaziale Internazionale), che vale circa 4 milioni di newton.

Inoltre la velocità dell’incrociatore all’impatto è di 648 Km/h, una velocità superiore a quella del treno più veloce del mondo, il Maglev (tale valore si ottiene dalla legge oraria della velocità del M.R.U.A., che in questo caso è data semplicemente da v=a･t, sostituendo si ha v=(18 m/s²)･(10 s)=180 m/s=648 Km/h). Ricordiamo inoltre che il risultato ottenuto è una sottostima del possibile risultato reale, giusto per ricordare quanto fosse “sgravato” questo personaggio. Forse, alla fin fine, è un bene che non sia più canonico.

E voi avete giocato a Il potere della Forza? Vi eravate mai chiesti quanto fosse realmente potente Starkiller? Fatecelo sapere nei commenti! E continuate a seguirci, anche su Facebook, YouTube, Instagram e Twitter! Vi terremo costantemente aggiornati sull’universo di Star Wars.